Utfordre etablerte sannheter

I forbedringsarbeid er det viktig å utfordre etablerte sannheter ved å stille spørsmål og etterlyse fakta.

Spørsmål gjør at vi utvikler oss og forbedrer oss.

Noen spørsmål kan oppfattes som kritikk, derfor er det viktig å holde fokus på prosess, ikke på person.

Om vi stiller spørsmål fordi vi er nysgjerrige og ønsker mer kunnskap, er det større sjangse for å bli hørt.  

En etablert sannhet innen Six Sigma er at en six sigma prosess medfører 3,4 feil for hver million muligheter. Det er en etablert sannhet som jeg vil utfordre.

Tabellen som går igjen i Six Sigma kurs og litteratur ser slik ut:

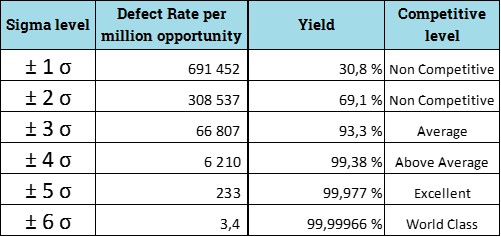
Statistisk prosess kontroll (SPC) benytter kontroll grenser til å skille mellom normal og spesiell variasjon. Kontrollgrensene representerer ± 3 sigma (σ) og inkluderer 99,7 % av dataene dersom dataene er normalfordelt.

Sannsynligheten for at en verdi er utenfor kontroll grensene er 0,3 % (100%-99,7%). Det samsvarer ikke med oppgitt verdi for 3 sigma i tabellen, som er 66 807 feil per million mulighet. Det burde vært ca. 3000 feil per million mulighet. 

Jeg bestemte meg derfor for å se litt nærmere på denne tabellen og får ingen av tallene til å stemme.

± 1 sigma inkluderer 68,26 % av dataene, sannsynligheten for å få en verdi utenfor er 31,74%.

± 2 sigma inkluderer 95,44 % av dataene, sannsynligheten for å få en verdi utenfor er 4,56%.

Det er imidlertid vanskeligere å finne sannsynligheten for at verdier er utenfor ± 4, 5 & 6 sigma. Statistiske tabeller oppgir ofte "tail area of unit normal distribution" (sannsynligheten for at en verdi er utenfor z sigma nivå) opptil z = 3,99. Jeg brukte z kalkulatoren fra denne nettsiden til å beregne sannsynligheten for at verdier er utenfor ± 4, 5 & 6 sigma, og får da følgende tabell:

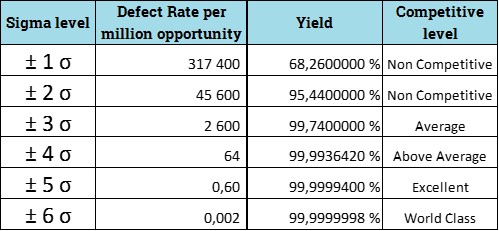
Som det fremgår av tabellen er feil rate for en prosess med ± 6 sigma 2 defekte per milliard mulighet.

Det er noe helt annet enn 3,4 defekter per million muligheter.

Dagens motto er: fortsett å still spørsmål.

Et utsagn blir ikke mer sant av å gjentas mange ganger. Et utsagn er sant så lenge det er basert på fakta.

Eller som wikipedia sier: "Et faktum er altså en sannhet med grunnlag i virkeligheten".

Vi kan ha ulike oppfatninger av virkeligheten. Derfor er det viktig å stille oppklarende spørsmål for å få et felles bilde av virkeligheten. 

Etter å ha delt denne artikkelen i en Lean Six Sigma gruppe på LinkedIn fikk jeg svaret fra Jud VanWyk: Det berømte 1.5 sigma prosess skiftet som benyttes for å korrigere for langtidsvariasjon. Du kan lese denne artikkel fra iSixSigma om 1.5 sigma prosess skiftet om du vil vite mer.

For å korrigere for langtidsvariasjon trekkes 1,5 sigma fra vår korttidsberegning av sigma. Når jeg sjekker z-verdien for 4,5 sigma, får jeg 3,4 feil per million muligheter. Hvis du har en kunde spesifikasjon som tilsvarer ± 4,5 sigma (både en øvre og en nedre spesifikasjon slik jeg har forutsatt i tabellene mine over) kan du forvente 7 feil per million muligheter. Takk til Jud for forklaringen!

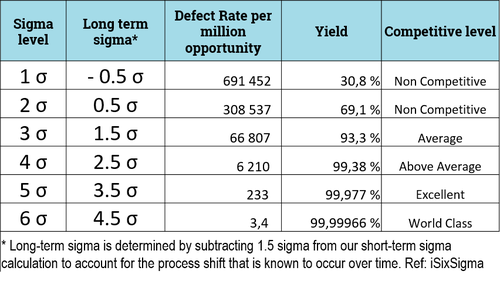
Her er en tabell som oppsummerer disse funnene (merk at tabellen er basert på kun en spesifikasjonsgrense, dersom du har både en nedre og en øvre spesifikasjon er antall defekte det dobbelte av det som fremgår av tabellen):